计算 (Calculation)

我们考虑攻击者试图生成一条比诚实链更快的备用链的情景。即使实现了这一点，也不会使系统开放于任意更改，例如凭空创造价值或获取从未属于攻击者的钱。节点不会接受无效的交易作为支付，诚实的节点也永远不会接受包含这些交易的区块。攻击者只能尝试更改他自己的某笔交易以取回他最近花费的钱。

诚实链与攻击者链之间的竞争可以被描述为一个二项式随机游走。成功事件是诚实链延长一个区块，增加其领先优势+1，失败事件是攻击者的链延长一个区块，减少差距-1。

攻击者从给定的差距中赶上的概率类似于赌博者破产问题。假设一个拥有无限信用的赌徒从一个亏损开始，并进行可能无限次的试验以试图达到收支平衡。我们可以如下计算他是否有可能达到收支平衡，或攻击者是否有可能赶上诚实链的概率[8]：

p = 诚实节点找到下一个区块的概率 q = 攻击者找到下一个区块的概率 q_z = 攻击者从落后 z 个区块的情况下赶上的概率

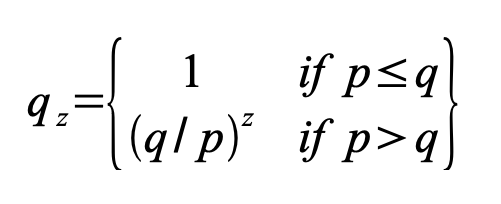
鉴于我们假设 p>q，随着攻击者需要赶上的区块数量增加，概率呈指数下降。由于赔率对他不利，如果他在早期没有幸运地迅速前进，随着他进一步落后，他的机会将变得微乎其微。

现在我们考虑新交易的接收者需要等待多长时间，才能充分确定发送者无法更改交易。我们假设发送者是一个攻击者，他希望让接收者相信他已经支付了一段时间，然后在一段时间后将支付切换回自己。接收者在这种情况发生时会收到警报，但发送者希望那时已经太迟了。

接收者在签名前不久生成一个新的密钥对并将公钥提供给发送者。这防止发送者通过持续工作提前准备好一条区块链，直到他足够幸运地超前，然后在那一刻执行交易。一旦交易被发送，不诚实的发送者就会秘密地在一条包含其交易替代版本的平行链上工作。

接收者等待直到交易被添加到一个区块中，并且在其后链接了 z 个区块。他不知道攻击者已经取得了多少进展，但假设诚实区块每个区块所需的时间是平均预期的，攻击者的潜在进展将遵循一个泊松分布，期望值为：

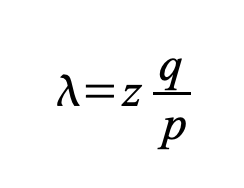
为了得到攻击者现在仍然可能赶上的概率，我们将他可能取得的每一进度量的泊松密度与他从那一点赶上的概率相乘：

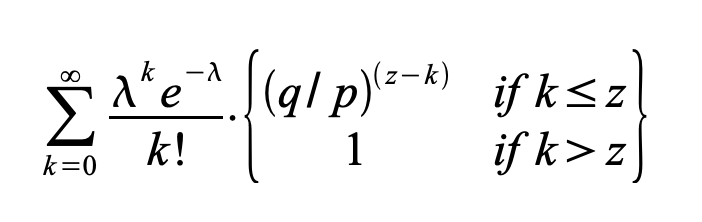
重新排列以避免对分布的无限尾部进行求和...

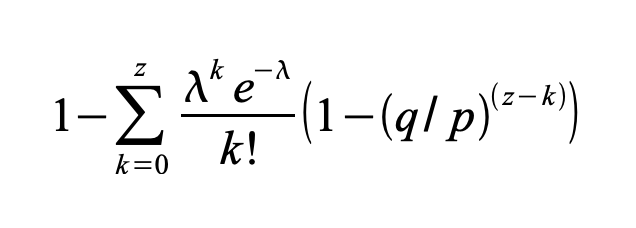
转换为 C 代码...

#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
 double p = 1.0 - q;
 double lambda = z * (q / p);
 double sum = 1.0;
 int i, k;
 for (k = 0; k <= z; k++)
 {
 double poisson = exp(-lambda);
 for (i = 1; i <= k; i++)
 poisson *= lambda / i;
 sum -= poisson * (1 - pow(q / p, z - k));
 }
 return sum;
}

通过运行一些结果，我们可以看到概率随着 z 呈指数级下降。

    q=0.1
    z=0 P=1.0000000
    z=1 P=0.2045873
    z=2 P=0.0509779
    z=3 P=0.0131722
    z=4 P=0.0034552
    z=5 P=0.0009137
    z=6 P=0.0002428
    z=7 P=0.0000647
    z=8 P=0.0000173
    z=9 P=0.0000046
    z=10 P=0.0000012

    q=0.3
    z=0 P=1.0000000
    z=5 P=0.1773523
    z=10 P=0.0416605
    z=15 P=0.0101008
    z=20 P=0.0024804
    z=25 P=0.0006132
    z=30 P=0.0001522
    z=35 P=0.0000379
    z=40 P=0.0000095
    z=45 P=0.0000024
    z=50 P=0.0000006

求解 P 小于 0.1%...

    P < 0.001
    q=0.10 z=5
    q=0.15 z=8
    q=0.20 z=11
    q=0.25 z=15
    q=0.30 z=24
    q=0.35 z=41
    q=0.40 z=89
    q=0.45 z=340