Cálculos (Calculation)

Consideramos el escenario de un atacante que intenta generar una cadena alterna más rápido que la cadena honesta. Incluso si esto se logra, no expone el sistema a cambios arbitrarios, como crear valor de la nada o tomar dinero que nunca perteneció al atacante. Los nodos no aceptarán una transacción inválida como pago, y los nodos honestos nunca aceptarán un bloque que las contenga. Un atacante solo puede intentar cambiar una de sus propias transacciones para recuperar el dinero que gastó recientemente.

La carrera entre la cadena honesta y la cadena del atacante puede caracterizarse como un Paseo Aleatorio Binomial. El evento de éxito es que la cadena honesta se extiende en un bloque, aumentando su ventaja en +1, y el evento de fracaso es que la cadena del atacante se extiende en un bloque, reduciendo la brecha en -1.

La probabilidad de que un atacante alcance desde un déficit dado es análoga al problema de Ruina del Jugador. Supongamos que un jugador con crédito ilimitado comienza en un déficit y juega potencialmente un número infinito de pruebas para intentar alcanzar el punto de equilibrio. Podemos calcular la probabilidad de que alguna vez alcance el equilibrio, o que un atacante alcance la cadena honesta, de la siguiente manera ^[8]:

p = probabilidad de que un nodo honesto encuentre el siguiente bloque q = probabilidad de que el atacante encuentre el siguiente bloque q_z = probabilidad de que el atacante alcance alguna vez desde z bloques de desventaja

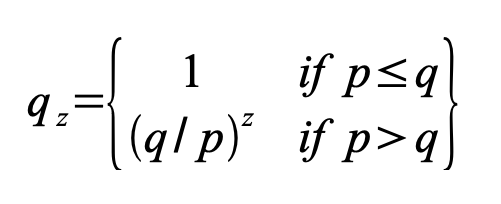
Dada nuestra suposición de que 𝑝>𝑞, la probabilidad disminuye exponencialmente a medida que aumenta el número de bloques que el atacante debe alcanzar. Con las probabilidades en su contra, si no realiza un intento afortunado de adelantarse al principio, sus posibilidades se vuelven insignificantes a medida que se retrasa más.

Ahora consideramos cuánto tiempo necesita esperar el destinatario de una nueva transacción antes de estar suficientemente seguro de que el remitente no puede cambiar la transacción. Suponemos que el remitente es un atacante que quiere hacer que el destinatario crea que le ha pagado por un tiempo, y luego cambiarlo para que se pague a sí mismo después de que haya pasado algún tiempo. El receptor será alertado cuando eso suceda, pero el remitente espera que sea demasiado tarde.

El receptor genera un nuevo par de claves y le da la clave pública al remitente poco antes de firmar. Esto evita que el remitente prepare una cadena de bloques por adelantado trabajando en ella continuamente hasta que tenga la suerte de adelantarse lo suficiente, y luego ejecute la transacción en ese momento. Una vez que se envía la transacción, el remitente deshonesto comienza a trabajar en secreto en una cadena paralela que contiene una versión alterna de su transacción.

El destinatario espera hasta que la transacción haya sido añadida a un bloque y se hayan enlazado z bloques después de ella. No conoce la cantidad exacta de progreso que ha hecho el atacante, pero asumiendo que los bloques honestos tomaron el tiempo promedio esperado por bloque, el progreso potencial del atacante seguirá una distribución de Poisson con un valor esperado de:

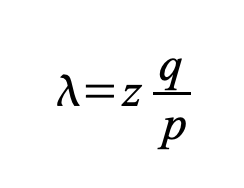
Para obtener la probabilidad de que el atacante aún pueda ponerse al día ahora, multiplicamos la densidad de Poisson para cada cantidad de progreso que podría haber hecho por la probabilidad de que pueda ponerse al día desde ese punto:

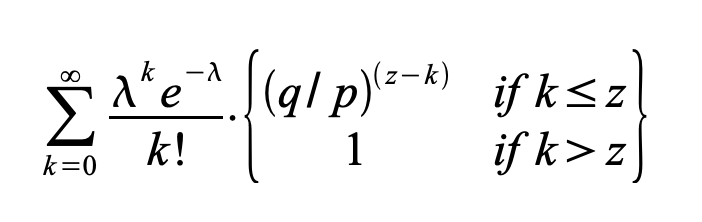
Reorganizando para evitar sumar la cola infinita de la distribución…

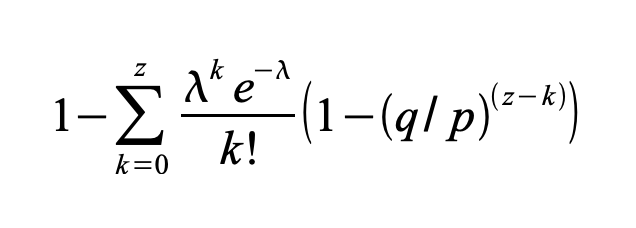
Convirtiendo a código C…

#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
 double p = 1.0 - q;
 double lambda = z * (q / p);
 double sum = 1.0;
 int i, k;
 for (k = 0; k <= z; k++)
 {
 double poisson = exp(-lambda);
 for (i = 1; i <= k; i++)
 poisson *= lambda / i;
 sum -= poisson * (1 - pow(q / p, z - k));
 }
 return sum;
}

Al ejecutar algunos resultados, podemos ver que la probabilidad disminuye exponencialmente con z.

    q=0.1
    z=0 P=1.0000000
    z=1 P=0.2045873
    z=2 P=0.0509779
    z=3 P=0.0131722
    z=4 P=0.0034552
    z=5 P=0.0009137
    z=6 P=0.0002428
    z=7 P=0.0000647
    z=8 P=0.0000173
    z=9 P=0.0000046
    z=10 P=0.0000012

    q=0.3
    z=0 P=1.0000000
    z=5 P=0.1773523
    z=10 P=0.0416605
    z=15 P=0.0101008
    z=20 P=0.0024804
    z=25 P=0.0006132
    z=30 P=0.0001522
    z=35 P=0.0000379
    z=40 P=0.0000095
    z=45 P=0.0000024
    z=50 P=0.0000006

Resolviendo para P menor que 0,1%…

    P < 0.001
    q=0.10 z=5
    q=0.15 z=8
    q=0.20 z=11
    q=0.25 z=15
    q=0.30 z=24
    q=0.35 z=41
    q=0.40 z=89
    q=0.45 z=340