COMU

계산

정직한 체인보다 더 빠르게 대체 체인을 생성하려는 공격자의 시나리오를 고려해보겠습니다. 설령 이러한 시도가 성공하더라도, 이는 무에서 가치를 창출하거나 공격자가 소유하지 않은 돈을 취득하는 등 임의로 시스템을 변경하는 것을 허용하지 않습니다. 노드들은 유효하지 않은 거래를 결제로 받아들이지 않으며, 정직한 노드들은 그러한 거래를 포함하는 블록을 절대 받아들이지 않습니다. 공격자는 오직 자신의 거래 중 최근에 지출한 돈을 되돌려 받기 위해 하나의 거래만을 변경하려고 시도할 수 있습니다.

정직한 체인과 공격자 체인 간의 경주는 이항 임의 보행(Binomial Random Walk)으로 특징지을 수 있습니다. 성공 이벤트는 정직한 체인이 블록 하나를 추가하여 우위를 +1만큼 늘리는 것이고, 실패 이벤트는 공격자 체인이 블록 하나를 추가하여 격차를 -1만큼 줄이는 것입니다.

주어진 열세에서 공격자가 따라잡을 확률은 도박꾼의 파산(Gambler's Ruin) 문제와 유사합니다. 무제한 신용을 가진 도박꾼이 열세로 시작하여 손익분기점에 도달하기 위해 잠재적으로 무한한 횟수의 시도를 한다고 가정해봅시다. 우리는 그가 언젠가 손익분기점에 도달하거나, 공격자가 정직한 체인을 따라잡을 확률을 다음과 같이 계산할 수 있습니다 ^[8]:

p = 정직한 노드가 다음 블록을 발견할 확률 q = 공격자가 다음 블록을 발견할 확률 q_z = 공격자가 z 블록 뒤에서부터 따라잡을 확률

eq1

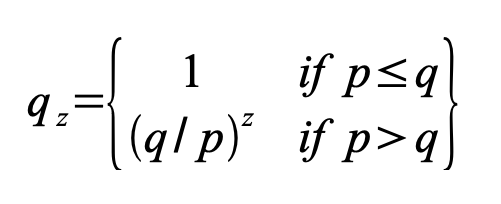
p > q라는 가정을 따르면, 공격자가 따라잡아야 하는 블록 수가 늘어날수록 그 확률은 지수적으로 감소합니다. 주어진 조건에서, 공격자가 초기에 운 좋게 앞서 나가지 못한다면, 뒤처질수록 그의 기회는 극히 작아집니다.

이제 수신자가 새로운 거래가 송신자에 의해 변경될 수 없다고 충분히 확신하기 위해 얼마나 오랫동안 기다려야 하는지 고려해보겠습니다. 우리는 송신자가 수신자로부터 일정 기간 동안 돈을 받은 것으로 믿게 만든 후, 일정 시간이 지난 후에 그 돈을 자신에게 되돌려받기 위해 거래를 변경하려는 공격자라고 가정합니다. 거래가 변경될 때 수신자는 경고를 받겠지만, 송신자는 그때가 너무 늦기를 바랍니다.

수신자는 새로운 키 쌍을 생성하고, 서명 직전에 송신자에게 공개키를 제공합니다. 이는 송신자가 미리 블록 체인을 준비하여 지속적으로 작업을 수행하고, 충분히 앞서 나가서 거래를 실행하는 것을 방지합니다. 거래가 한 번 발신되면, 이 부정직한 송신자는 몰래 자신의 거래를 대체하는 버전의 블록 체인 작업을 병행하여 시작합니다.

수신자는 해당 거래가 블록에 추가되고 그 이후에 z개의 블록이 연결될 때까지 기다립니다. 그는 공격자가 얼마나 많은 블록을 생성했는지 정확히 알지 못하지만, 정직한 블록들이 블록당 평균 예상 시간을 따른다고 가정하면, 공격자의 잠재적 진척도는 기대값이 있는 푸아송 분포(Poisson distribution)에 따르게 됩니다:

eq2

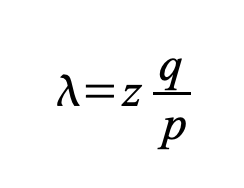
현재 공격자가 여전히 따라잡을 수 있는 확률을 얻기 위해, 그가 해당 시점부터 따라잡을 수 있는 확률로 만들어낼 각 진척 규모별 푸아송 밀도를 곱합니다:

eq3

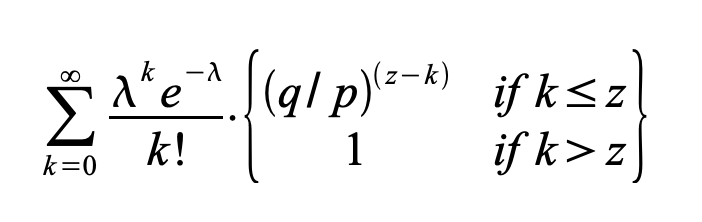
분포에서 무한하게 합산하지 않도록 정리하면 아래와 같습니다.

eq4

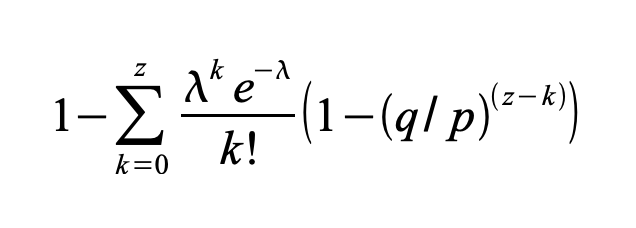
위를 C코드로 변환하면 아래와 같습니다.

#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
 double p = 1.0 - q;
 double lambda = z * (q / p);
 double sum = 1.0;
 int i, k;
 for (k = 0; k <= z; k++)
 {
 double poisson = exp(-lambda);
 for (i = 1; i <= k; i++)
 poisson *= lambda / i;
 sum -= poisson * (1 - pow(q / p, z - k));
 }
 return sum;
}

결과를 실행하면, z에 따라 지수적으로 감소하는 확률을 볼 수 있습니다.

    q=0.1
    z=0 P=1.0000000
    z=1 P=0.2045873
    z=2 P=0.0509779
    z=3 P=0.0131722
    z=4 P=0.0034552
    z=5 P=0.0009137
    z=6 P=0.0002428
    z=7 P=0.0000647
    z=8 P=0.0000173
    z=9 P=0.0000046
    z=10 P=0.0000012

    q=0.3
    z=0 P=1.0000000
    z=5 P=0.1773523
    z=10 P=0.0416605
    z=15 P=0.0101008
    z=20 P=0.0024804
    z=25 P=0.0006132
    z=30 P=0.0001522
    z=35 P=0.0000379
    z=40 P=0.0000095
    z=45 P=0.0000024
    z=50 P=0.0000006

0.1% 미만의 P를 풀면 아래와 같습니다.

    P < 0.001
    q=0.10 z=5
    q=0.15 z=8
    q=0.20 z=11
    q=0.25 z=15
    q=0.30 z=24
    q=0.35 z=41
    q=0.40 z=89
    q=0.45 z=340

계산